Site Title

“Education is the passport to the future, for tomorrow belongs to those who prepare for it today.”

Malcomb X

Introduction about myself

I have been in the worked in the engineering field for 23 years. I have obtained a bachelors degree, a masters degree in engineering and I am currently working on my PHD in engineering. I have studied mathematics, calculus, differential equations, partial differential equations, chemistry, electrochemistry, physics, thermodynamics, fluid mechanics, heat transfer, batteries and fuel cells.

I guess you can say that learning is my passion, I also enjoy sharing my knowledge and wisdom with people to make the world a better place. I guess I should have gone into teaching instead of engineering.

The main reason I am doing this blog is to share knowledge on the following:

how does is work, how do I use it and also help decide on which technology to select in some instances. For example can I select a heat pump over a furnace.

I will also take the knowledge and look at do costing exercises.

We will pick up a lot along the journey. I hope you join in. I hope you learn along the way

Agenda:

• Discussion of Math (Calculus, Derivative, Integrals (single, double and triple), and mean value theorem
• Applications of Math
• Numerical Methods
• Conservation of Energy
• Ways Energy can be stored
• Conservation of Mass/Species
• Conservation of Momentum
• Governing Equations for Computational Fluid Dynamics (CFD)
• Second Law of Thermodynamics
• Applications of Second Law
• Maxwell Relationships
• Chemistry and Electrochemistry

The following will be the tools that we use to tackle everyday items such as hot water heaters, furnaces, batteries, fuel cells , pumps and fans.

I am also looking for topics that you would like to cover and answer your questions.

Something to think about before we start our calculus lesson, believe it or not we know calculus in some form. For instance our understanding formulas of linear equations come from calculus and the arc length formula s=r*theta come from calculus too.

Our physics formulas also come from calculus too.

One of the hopes from this series is help build a fundamental understanding of chemistry, physics, and engineering. Eventually we will all be able to understand how everything works and then how do I use it.

Thank you for your time.

Lesson Number 1 – The lead into the material. My thoughts on math

A long time ago, my sixth grade teacher gave us challenge I have not forgotten to this day. His challenge was simple, think of a job that does not require math. Mr. Willis and the class argued for 30 mins and no matter what happens the jobs requires math. I saw the lesson Mr. Willis was trying to teach us, math is one of most important tools/skills we can develop and learn. With math you can tackle any problem and solve it. I consider it the base of my engineering career.

I personally think of math is a language, it allows us to establish relationships between variables, it allows us to predict behavior in systems. Math also allows use communicate across different languages.

My next steps will be to start the lessons on math, if you would like to contact me to discuss a topic or request a topic please let me know. Thermodynamics is everywhere!!

First Actual Lesson the Derivative ( In Progress)

The most fundamental concept of calculus is the derivative. What is a derivative? The derivative is simply the rate of change of a function. All of our understanding of linear equations come from calculus.

This fundamental concept is used in numerical methods, I will tackle this in a future lesson. it is used physics for the relationship of position (x or y), velocity and acceleration, in electrical engineering to relate charge (q) and current(i or j).

Side note- electrical engineering like using “i” for current, and chemical engineering use “j” for current.

The derivative of a single variable system is shown below,

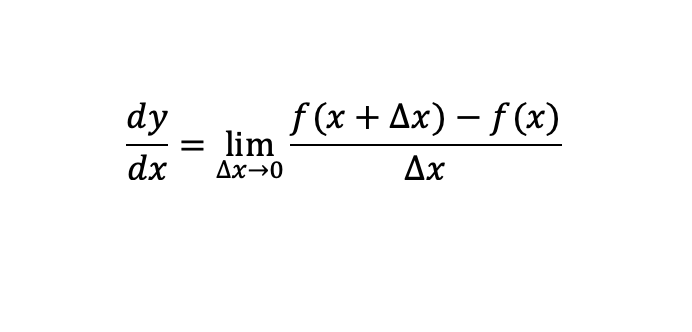
The derivative is the slope of a tangent line at any point:

Below is the formula for the slope of a linear line, not that there is no limit goes to zero.

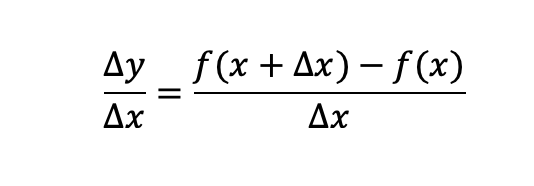
I am working the best way to put my thought in the blog, I am open to suggestions, so please feel free to comment.

I will continue with cases of derivative of polynomials, I will even help with memorizing trig derivatives and help with the chain rule.

Thank you for your time! I hope you enjoy.

Sample Derivative of a Polynomial Term

The first type of derivative we need to examine is of a polynomial term. We are going to examine y=x^2.;

We are going to use the formula for the derivative to set up step 1

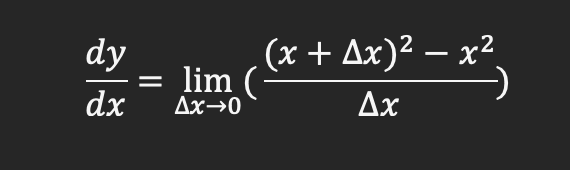
The first term needs to be expanded, one of the best tools to use for other higher power functions is Pascal’s triangle I have enclosed a link https://www.mathsisfun.com/pascals-triangle.html

Like the website I hope I make engineering fun.

If we expand the polynomial we get the following

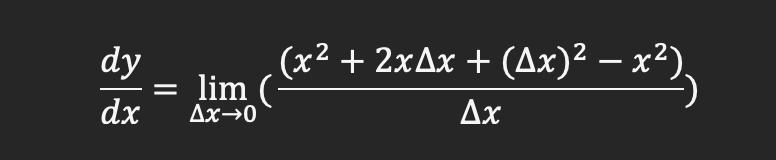
If we reduce we will get the following:

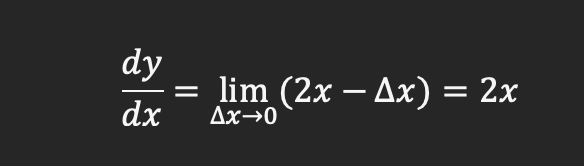
For a generic case for a polynomial we get the following:

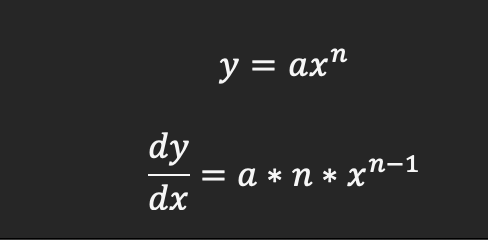
This is true for any n including zero.

The next case I will go through will be the y=sin(x), then get to the product rule, quotient rule.

Please let me know if there is something you want me to cover. Keep in mind I am building up the toolbox to handle any problem we are faced with.

Update and derivative of y=sin(x)

My apologies it has bee a while since I have updated, I have had a few items to take care of pending to work, school and home. I am going to be doing updates over the holiday break. Like I said before this is my first blog and I am using this for people who have a passion for knowledge. I have been a person who likes to know how things work.

I would like some feedback on what is the best way to get knowledge out there, would you prefer a video, a powerpoint or the current way? Please feel free to make suggestions. Also I will eventually get into my fuel cells papers that are published.

I am posting below the derivative of the y=sin(x)

In conclusion, the derivative of y=sin(x) simplifies to cos(x)

Derivative of the y=cos(x)

I am sending a screen shot of the y=cos(x) derivation.

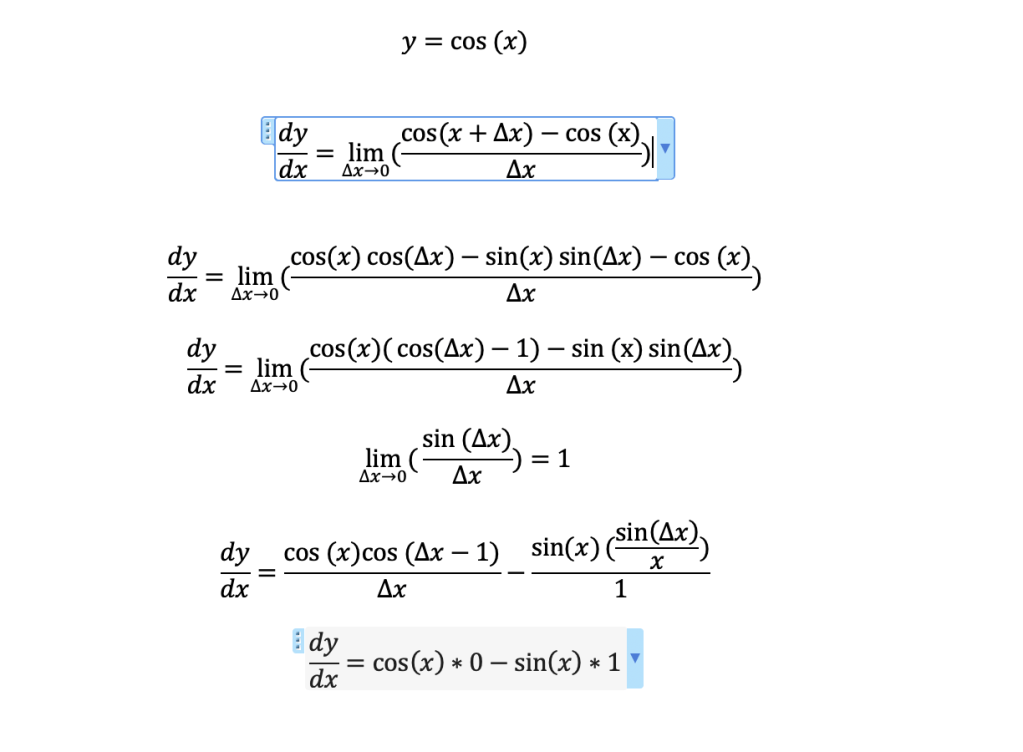
Happy Holidays everyone, I am going to tackle the product rule next and the chain rule I am sorry that this is moving slow, keep in mind for those Star Wars fan Episode 1-3 built the frame work for 4-6. We are in the prequels right now. Once we get through the fundamentals we will tackle big items like heat pumps, batteries, fuel cells and everywhere thermo is used.